数据结构
树与二叉树
节点拥有的子树的数量称为节点的度,树的度是树内各节点度的最大值
节点的层次从根开始定义,根为第一层
树中节点的最大层次称为树的深度(高度)
如果将树中节点的各子树看成从左到右是有次序的,称该树为有序树,否则为无序树
二叉树的左右子树其次序不能交换!
二叉树的性质:
(1)在二叉树第 $i$ 层至多有 $2^{i-1}$ 的节点($i \ge 1$)。
(2)深度为 $k$ 的二叉树至多有 $2^k-1$ 的节点($k \ge 1$)。
(3)叶子节点数 = 度为 2 的节点数 + 1($n = n_1 + 2n_2 + 1 = n_0 + n_1 + n_2$)。
(4)具有 $n$ 个节点的完全二叉树的深度为 $\lfloor log_2{n} \rfloor + 1$。
顺序存储结构适合完全二叉树
线索二叉树:

树的路径长度是从树根到每一节点的路径长度之和
哈夫曼树中,任一字符的编码不能是另一字符编码的前缀,并且没有度为 1 的节点!
含有 $n$ 个节点的不相似的二叉树有 $\frac{1}{n+1} \binom{2n}{n}$ 棵!(卡特兰数)
图
弧尾(初始点)弧头(终端点)
简单路径:顶点不出现重复的路径
连通分量指无向图中的极大连通子图(森林与树的关系)
有向图中的极大强连通子图称为有向图的强连通分量
构造一个具有 n 个顶点和 e 条边的无向网 G 的时间复杂度为 $O(n^2+e\cdot n)$
在建立邻接表或逆邻接表时,若输入的顶点信息即为顶点的编号,则建立邻接表的时间复杂度为 $O(n+e)$,否则,需要通过查找才能得到顶点在图中位置,则时间复杂度为 $O(n\cdot e)$。
假若在删去顶点 v 以及和 v 相关联的各边之后,将图的一个连通分量分割成两个或两个以上的连通分量,则称顶点 v 为该图的一个割点(关节点)。一个没有割点的连通图称为重连通图。重连通图上,任意一对顶点之间至少存在两条路径,则在删去某个顶点以及依附于该顶点的各边时也不破坏图的连通性。若在连通图上至少删去 k 个顶点才能破坏图的连通性,则称此图的连通度为 k。
查找
顺序查找的平均查找长度为 $\frac{(n+1)}{2}$,当查找不成功的情况不能忽视时,查找算法的平均查找长度是查找成功时与查找不成功时的平均查找长度之和。
对于顺序查找,不论给定的关键字如何,查找不成功与给定值进行比较的关键字个数均为 $n+1$。假定查找成功与不成功的可能性相同,对每个记录查找的概率也相同$(P_i = \frac{1}{2n})$,此时平均查找长度为 $\frac{3}{4} (n+1)$。
折半查找法在查找成功时和给定值进行比较的关键字个数至多为 $\lfloor log_2n \rfloor + 1$,不成功时最多也不会超过该值。
查找成功时,折半查找的平均查找长度为 $\frac{n+1}{n} log_2{(n+1)}-1$,当 $n$ 较大 $(n > 50)$ 时,近似为 $log_2{(n+1)}-1$。
长度为 $n$ 的表均匀地分成 $b$ 块,每块含有 $s$ 个记录($b = \lceil \frac{n}{s} \rceil$),分块查找的平均查找长度为 $\frac{b+1}{2} \cdot \frac{s+1}{2}$。如果用折半查找确定所在的块,平均查找长度约为 $log_2{(\frac{n}{s}+1)}+\frac{s}{2}$。

排序
有序的顺序表折半查找的 ASL = $log_2{(n+1)}-1$。
直接插入排序所需进行关键字间的比较次数和移动记录的次数约为 $\frac{n^2}{4}$,时间复杂度为 $O(n^2)$。
折半插入排序所需附加存储空间和直接插入排序相同,仅减少了关键字间的比较次数,而记录的移动次数不变,时间复杂度为 $O(n^2)$。
希尔排序(缩小增量排序):增量序列需要保证增量序列中的值没有除 1 之外的公因子,并且最后一个增量值为 1。
冒泡排序:时间复杂度为 $O(n^2)$。
快速排序:最适合选用顺序存储方式,原始数据基本有序时,时间复杂度趋于 $O(n^2)$。
选择排序:简单选择排序、树形选择排序、堆排序(堆排序仅需一个记录大小供交换用的辅助存储空间)
归并排序:时间复杂度为 $O(nlogn)$,需要和待排记录等数量的辅助空间。
(与快速排序、堆排序相比,归并排序最大特点是稳定)
基数排序:借助多关键字排序的思想对单关键字进行排序的方法,为稳定排序。
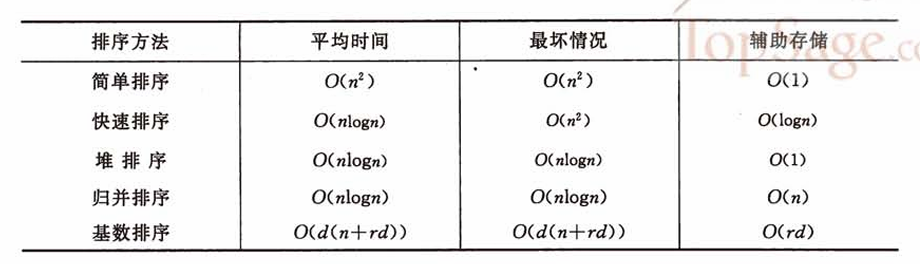
(简单排序不包括希尔排序,所有时间复杂度为 $O(n^2)$ 的简单排序法也是稳定的,而快速排序、堆排序、希尔排序等时间性能较好的排序方法都是不稳定的)
根据完全二叉树的性质,最后一个非叶子节点是 $⌊n/2⌋$。
